量子コンピュータ
石井俊雄
コンピューターの処理速度は年々伸び続け、スーパーコンピューターは1秒間に10の15乗回もの計算をこなすようになった。
だがそれでもコンピュータで計算しきれない問題は沢山ある。
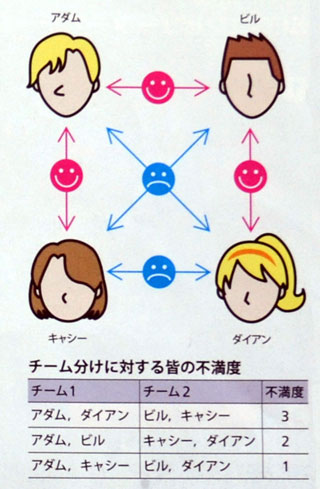
簡単な例を1つ挙げよう。スポーツ同好会で、メンバーが2チームに分かれて試合をするとする。各チームには何人ずつ所属してもいいが、
一部のメンバー同士は仲が良く、それ以外は険悪だ。不満を最小限に抑えるため、仲良しができるだけ同じチームに所属できるように配慮したい。
どのように分ければいいだろうか?
1つの方法は、全ての分け方について、どれ位不満が出るかを点数化することだ。仲良しどうしが分かれるごとに不満度を1点加算し、合計点を比べて、
最小となる組み合わせを採用すればよい(右図参照)。
例えば、表の最初の行は、アダムとビルは仲がいいのにチームは分かれたから不満度が1、更に、アダムとキャシーは仲がいいのにチームは分かれたから不満度が1、
そして、ダイアンとビルは仲がいいのにチームは分かれたから不満度が1で、これ等を足し合わせると不満度が3となる。
2行目、3行目も同様の計算をすれば表に示した不満度が算出される。
かくしてこの場合の最適チーム分けの解は3行目の組み合わせとなる。
この方法はメンバーが4人なら簡単だが、数が増えると途端に難しくなる。チーム分けの方法が、メンバー数とともに急増するためだ。
「難しい」という言葉は、計算機学では、
扱う数字が少し大きくなるだけで問題を解くのに必要な計算時間が爆発的に長くなる(指数関数的に増大する)ことを意味する。
即ち、「扱う数字」がある数(1以上の)のべき乗のところに出てくる計算式で「計算時間」が決定される場合が問題なのだ。
ちなみに、この場合の「計算時間」を「指数関数時間」と呼ぶ。
もう1つ、それに対抗する形の時間として「多項式時間」というのがある。
それは、「扱う数字」が「底」のところに出てくる計算式、即ち多項式で「計算時間」が決定される場合の「計算時間」を云う。
仮に、ある1つのチーム分け方法について、コンピュータで不満度を計算するのに1ナノ秒(10-9秒)かかるとしよう。1チーム30人なら、約1秒で全ての分け方について不満度を調べられる。
だが50人いたら、宇宙の年齢である137億年間、計算し続けても答が出ない。
この問題は、専門的には「グラフ分割問題」と呼ばれ、いわゆるNP完全問題の1つだ。扱う数が増えると必要な計算が爆発的に増加し、正攻法で解こうとすると確実に破綻する。
だが、実は、全てのケースについて不満度を計算する必要はない。目的は不満度が最小となるチーム分けを知ることで、他の場合についてはどうでもいいからだ。

そのような狙いで高速計算する方法を考えて、浮かび上がったのが、右図の「不満度シミュレーター」で示すアイディだ。
実際にどんな物理系を作ればいいのか。簡単のために、4人のメンバーを2人ずつのチームに分ける場合を考えよう。
先ず4人のメンバーに対応する4つの容器を用意し、その中に粒子を1個ずつ入れる。粒子は「スピン」と呼ばれる性質を持つ小さな棒磁石のようなもので、
その方向が所属するチームを表す。スピンが上向きならチーム1、下向きならチーム2だ(右図参照)。
アダムとビルがチーム1、キャシーとダイアンがチーム2に所属している。
これをシミュレーターで表すと、アダムとビルの粒子がスピン上向き、キャシーとダイアンの粒子がスピン下向きになる。
各人の不満度を計算するには、ほかの3人の粒子のスピンを夫々計測し、これと反対向きの磁場を足し合わせて加える。但し相手と仲が悪い場合は強い磁場Xを、
良い場合は弱い磁場Yをかける(X>Y)。
今、アダムの粒子にかかる磁場を考えよう。アダムはビルとは仲がいいので強さYの磁場を、ビルのスピンとは逆の下向きにかける。
キャシーとも仲がいいのでやはり強さYの磁場を、キャシーのスピンとは逆の上向きにかける。
一方ダイアンとは仲が悪いので、強さXの磁場をダイアンのスピンとは逆の上向きにかける。
全部足すとビルとキャシーの磁場は相殺し、ダイアンの上向きの磁場Xが残る。
ある粒子と反対向きの磁場をかけるというのは、その粒子と同じチームになるのに障壁を設けることに相当する。
同じチームになるにはこの障壁を乗り越えるので、その分だけ粒子のエネルギーが高くなる。
仲の悪い人の磁場Xが仲のいい人の磁場Yより大きいということは、仲が悪い人と同じチームになると粒子のエネルギーがより高くなることを意味する。
従って、粒子のエネルギーは、その人の不満度を示す。
今、最終的にアダムにかかる磁場は上向きで、全体としてチーム1に入る力が強い。
アダムはその通りチーム1に所属しているので、トータルの障壁はマイナスになり、アダムの粒子はXだけエネルギーが下がる。
上の表のチーム分けごとに同様の操作をし、全ての粒子のエネルギーを足し合わせ、シミュレーターのエネルギーを求めると、XとYの値を適当に選ぶことで、
チーム分けに対する不満度の表(上の表)と一致することがわかる。
この不満度の表(上の表)と一致することを実際の計算で示そう。
なお、何れの場合も、A,B,C,Dはアダム、ビル、キャシー、ダイアンを示す。
括弧内の+はスピン上向きを、括弧内の−はスピン下向きを、示す。
+Yは上向きの磁場Yを、-Yは下向きの磁場Yを、+Xは上向きの磁場Xを、-Xは下向きの磁場Xを、示す。但し、X>Y。
(1)上の表の1行目の場合の磁場の掛合いの結果を表に示す。
| | A(+) | B(-) | C(-) | D(+) | total |
| A(+) | | +Y | +Y | -X | -X+2Y |
| B(-) | -Y | | +X | -Y | +X-2Y |
| C(-) | -Y | +X | | -X | -Y |
| D(+) | -X | +Y | +X | | +Y |
上から2行目の左から3列目のセル(「枡」のこと。)に書込む値について説明する。
1行目の3列目のセルのB(-)はチーム2に属しているので下向きのスピンを持つことを示している。
2行目の左端のセルのA(+)はチーム1に属しているので上向きのスピンを持つことを示している。
このA(+)に対し1行目の3列目のセルのB(-)は、自分のスピンの向きの反対方向の磁場を掛けるが、AとBは仲がいいので2行目の3列目のセルの値は+Yとなる。
以下、同様にして展開した。
(2)上の表の2行目の場合の磁場の掛合いの結果を表に示す。
| | A(+) | B(+) | C(-) | D(-) | total |
| A(+) | | -Y | +Y | +X | +X |
| B(+) | -Y | | +X | +Y | +X |
| C(-) | -Y | -X | | +X | -Y |
| D(-) | -X | -Y | +X | | -Y |
(3)上の表の3行目の場合の磁場の掛合いの結果を表に示す。
| | A(+) | B(-) | C(+) | D(-) | total |
| A(+) | | +Y | -Y | +X | +X |
| B(-) | -Y | | -X | +Y | -X |
| C(+) | -Y | +X | | +X | +2X-Y |
| D(-) | -X | +Y | -X | | -2X+Y |
磁場を掛け合った結果、システム全体のエネルギートータルは次表の通り。
(「計算式」欄の括弧の前の符号は、当該容器の所属チームのスピンの向きの反対の符号を示す。例えば、
(1)のAの場合は、Aの所属チームはチーム1(スピンの向きは上向き)だから符号はその反対の'-'となる。
また、括弧内は、当該容器に掛けられた磁場のtotalの値(「total」欄の値」)である。)
| チーム分けの場合 | チーム1 | チーム2 | 計算式 | エネルギー | X=5,Y=1とすると |
| (1)の場合 | A・D | B・C | -(-X+2Y)-(+Y)+(+X-2Y)+(-Y) | +2X-6Y | 4 |
| (2)の場合 | A・B | C・D | -(+X)-(+X)+(-Y)+(-Y) | -2X-2Y | -12 |
| (3)の場合 | A・C | B・D | -(+X)-(+2X-Y)+(-X)+(-2X+Y) | -6X+2Y | -28 |
以上により、全ての粒子のエネルギーを足し合わせ、シミュレーターのエネルギーを求めると、XとYの値を適当に選ぶ(但し、X>Y)ことで、
チーム分けに対する不満度の表(上の表)と一致することがわかる。従って、このシミュレーターの正しさが確かめられたと云える。
システム全体は冷却されるので、その過程で仮令エネルギー状態が高いチーム分けの状態が存在したとしても、冷却に伴ってその状態は破綻し、
最終的にエネルギーが最低の状態で安定する。
その状態は、この例では、3番目の状態(エネルギーが最低の−28)なのだ。
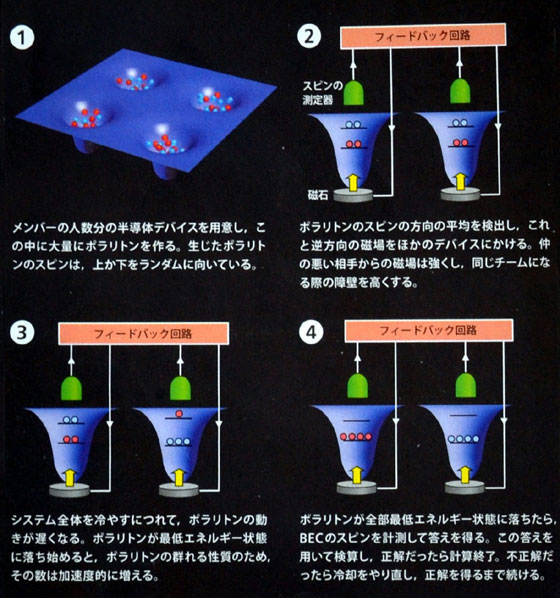
実物のシミュレーターでは、容器としてボーズ・アインシュタイン凝縮(BEC:Bose-Einstein condensation)が生成される半導体を使用する。
容器にスピンの向きの測定装置と、粒子に磁場をかける装置をつけておく。
各粒子には、周囲の粒子夫々のスピンと反対方向の磁場を足し合わせて加える。磁場の大きさは、夫々の粒子との人間関係によって決める。
スピンには磁場と同じ方向を向きたがる性質がある。ある粒子のスピンと反対方向の磁場をかけるというのは、その粒子が属しているチームに入るのに障壁を設けることに相当する。
これを乗り越えて同じチームに入る、つまり同じ方向にスピンを向けると、その分だけ粒子のエネルギーは高くなる。
エネルギーの増分は、加えられた磁場の強さに比例する。仲の悪い人の粒子にかける磁場を、仲の良い人の粒子のためにかける磁場より強くすれば、
仲の悪い人と同じチームになった時、粒子のエネルギーがより高くなる。つまり粒子のエネルギーが、その人の不満度を反映する。
システム全体のエネルギーは、4つの粒子のエネルギーの和だ。相性の悪い人どうしが同じチームに入る率が高いほど、システム全体のエネルギーが高くなる。
今、このチームには「仲の良い人」と「仲の悪い人」しかおらず、「どっちでもない人」がいないので、この値はそのまま、仲の良い人どうしが別々のチームに分かれる不満度になる。
こうしてメンバー全員の不満度を、システムのエネルギーで表すシミュレーターが構築できる。メンバーの数を増やすには、容器の数を増やせばよい。
最初の述べた50人で爆発したスーパーコンピュータによる計算時間が、ここでは台数を増やすだけで短時間のうちに終了するのだ。
図中、「ポラリトン」とあるのは、半導体にレザーを照射すると、半導体の中に「エキシトン・ポラリトン」という粒子が大量に生じる。
この粒子はボーズ粒子(光子のこと。光はミクロの世界では粒子として振舞うのだ。)で低温(現在約10K、-266℃)でBECになるが、その「エキシトン・ポラリトン」のことで、単に「ポラリトン」と呼んだものだ。
このシミュレーターはつまるところ、冷やすことでチーム分け問題の答を出すコンピュータだ。
その計算時間は、演算の回数ではなく、シミュレーターを冷却し粒子を最低エネルギーまで落とし込む時間で決まる。
問題は、実際にどれ位時間がかかるかだ。
これまで各容器に粒子が1個入っているとの前提で話を進めてきたが、粒子1個の運動エネルギーを奪って温度を下げていくのは、不可能ではないにせよ長い時間がかかる。
ここで登場するのがBECだ。
容器(実際は「量子井戸」という現象を使用する)の中に、100万個以上のボーズ粒子を入れてBECした状態で冷却すると、
粒子1個のときより100万倍の速さで最低エネルギーまで落とし込むことが出来る。
シミュレーターの中の半導体にレザーを照射して、その中の量子井戸にBECを生成し、装置全体を冷却して、
BECしたボーズ粒子が最低エネルギーに落とし込まれたら、計算終了だ。
シミュレーターの中の容器同士は、フィードバック回路で互いに連結されているので、
シミュレーター全体が冷却される過程で互いに磁場を掛け合うことで相互作用しながら、別の言葉で言えば互いに会話しながら、最低エネルギーへと落ち込んでいく。
最低エネルギーに落ち込んだ状態で、各容器のスピンを計測すれば、上向きのスピンを示す容器を当てられた人はチーム1、
下向きのスピンを示す容器を当てられた人はチーム2となり、チーム分けの答が得られるのだ。
常に正しい答が得られるとは限らないので、コンピュータを何度でも走らせ、得られた結果の中で最もエネルギーの低いものを選び、もとの問題に代入して検算する。
正解だったら計算終了。不正解なら冷却をやり直し、正解が得られるまで続ける。
検算の計算量は爆発しないので、冷却を繰り返しても高速で答が出せる。
これが、量子コンピュータの動作原理だ。実験室段階であっても、実際稼動している物(ぶつ)が存在していることに感銘を受ける。
何故なら、従来のノイマン型コンピュータとは全く異なる動作原理に従って答を出すからだ。
従来のノイマン型コンピュータの動作原理は逐次処理というものだ。即ち、結果を得るためのアルゴリズムを作成し、
それをプログラム(コンピュータへの指令を順番に並べること)して、コンピュータに実行させるものだ。
その実行は逐次処理型だから、プログラムの中の指令を1つづつ順番に処理、即ち逐次処理するのだ。
だが、この新しい型の量子コンピュータはそんなことはしない。
量子現象を利用して高速に計算するのだ。
アルゴリズムに従って演算を重ねていくものではなく、自然法則の力を借りて一気に答に到達する新しいコンピュータだ。
これが驚きでなくて何だろう。
このBEC応用の量子コンピュータではチーム分け問題以外は解けないのではないかと思われるかも知れないが、そんなことはない。
NP完全問題とは、複数の場所を結ぶ最短経路の探索など、一定の制限下で最適解を探す問題の一種だ。
医薬品や新材料の開発、機械構造や電子回路の設計、配送ルートの計画など、様々な場面で必要になる。
だが、扱う数が少し大きくなるだけで計算量が爆発的に増大し、厳密に解くのは難しい。
だが、その中の1つが高速で解ければ、数学的変換で他の問題も高速で解ける可能性があり、大きな社会的インパクトとなるだろう。
(詳しくは日経サイエンス2011/3を参照ください。) '
この話で面白いのは、環境に対応することが出来る素子を複数個用意し、それらを互いにある通信路で結んだ、
ある種のネットワーク・システム(「NS」と呼ぶ。)を考えた場合、
環境の変化に各素子は対応するが、その結果、NS全体としてはどうなるのだろう?ということだ。
例えば、脳を考えた場合、脳細胞と云う素子とシナプスという通信路により出来上がるNSはどう振舞い、どう安定するのだろう?・・・と云う疑問が生じる。
この場合、ある学習で形成されたか細いNSは、寝ている間という外部環境下で最低エネルギー状態に曝される。
その結果、最低エネルギーという外部環境に耐えられない通信路は死滅し、耐えた通信路は生残り翌日の学習でより拡幅増強された通信路に成長する?
・・・そんなストーリーがあるかも知れない。
となると、「グラフ分割問題」と「最短経路の探索」とは繋がっていることになる。何故なら、シナプスによるネットワークの連結は、
複数の場所を結ぶ最短経路の探索というNP完全問題の一種そのものと思われるからだ。
だけど、そんなストーリーがあるとしたら、「寝る子は太る」ってどんなこと?・・・そのNSが腹部で形成された場合のことかも知れない!
・・・そう云えば、小生、子供の頃は少し太り気味だったな!今とは違って。君たちには想像も出来ないことだろうが。
・・・頭に出来ないでお腹に行っちゃったのかも!
そんなに思うと、昔が懐かしい。
特に若葉のころが。・・・仮令、太り気味でも・・・。
First Of May (1969年)
作曲:THE BEEGEES
作詞:THE BEEGEES
When I was small
And Christmas trees were tall
We used to love while others used to play
Don't ask me why
The time has passed us by
Someone else moved in from far away
Now we are tall
And Christmas trees are small
And you don't ask the time of day
But you and I our love will never die
But guess who cried come first of May
The apple tree that grew for you and me
I watch the apples falling one by one
・・・
コメントはこちらへメールして下さい。その際、文中冒頭に「HPコメント」と記して下さい。
Email
<コメント欄> 当欄は上記のメールをコメントとして掲示するものです。


